
REED-SOLOMON CODING
In telecommunications, Reed–Solomon (RS) codes are a kind of channel coding techniques operating on blocks of data treated as a set of finite field elements, called symbols. By adding t redundancy symbols to the data, RS codes can detect (but not correct) any combination of up to t erroneous symbols, or locate and correct up to and including t/2 erroneous symbols at unknown locations. As better explained below, RS codes are especially suitable for multiple-burst errors correction, since consecutive corrupted bits affect just a limited number of symbols [4].
In this project, after a short recap of general theory, the error-correction capability of RS codes is discussed and analyzed. First, a MATLAB script (without employing any of its built-in functions) for Reed-Solomon (RS) encoding and decoding is proposed. Then, the same algorithm is adapted for a much more efficient C/C++ implementation.
The developed encoder / decoder pair can handle extended Galois field degrees m from 3 up to 8. The primitive polynomials f (x) selected for the definition of each finite field are [1]

To obtain the mapping table between symbols and m-bit streams (aka basis), the former are converted into polynomials and divided by the primitive polynomial. Then, the remainder of this division represents the basis corresponding to the starting symbol [1]. In Fig.1 and Fig.2 the mapping table for m = 3 and 4 are depicted. The next and essential step is to create functions for executing basic arithmetic operations (addition, multiplication and power) within each Galois field (GF).
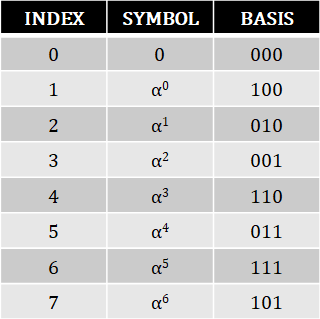
Fig.1 - Mapping table between symbols and basis for m = 3

Fig.2 - Mapping table between symbols and basis for m = 4
As well known, RS are nonbinary cyclic codes with symbols made up of m-bit sequences, with m > 2. As a special subclass of the BCH ones, the RS codes are typically expressed in the conventional form
where n is the codeword symbol-length, k the message symbol-length and t the maximum number of symbol errors correctable by the code (and, thus, 2t represents the number of parity symbols).
The encoder works in systematic form, appending the redundancy bits at the beginning of the codewords. The parity symbols are calculated by upshifting the input message polynomial by 2t positions and then dividing by the generator polynomial g(x), which in turn can be easily estimated as

On the decoder side, after the bit-to-symbol conversion the coefficients of the syndrome polynomial S(x) are computed as
where i varies from 1 to 2t and r(x) represents the received codeword polynomial, which can be thought as the sum of the transmitted codeword polynomial c(x) and the error polynomial e(x). The presence of errors is detected if at least one of these coefficients proves to be different from zero.
In this case, the correction procedure has to determine both location and magnitude of the errors. In order to do so, first the Berlekamp-Massey algorithm [3] is executed for estimating the error locator polynomial σ(x) by iteratively computing the discrepancy Δ as

where σi is the i-th degree coefficient of σ(x), j the current (out of 2t) iteration of the algorithm and E the number of estimated errors so far.
Moreover, since the polynomial σ(x) is related to the error locations Li of e(x) by the relation
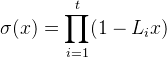
it clearly appears that Li can be obtained as the reciprocal of the roots of σ(x) by using the Chien search algorithm [2]. Next, the error evaluator polynomial ω(x) is introduced by solving the Key Equation
since it is essential for the estimation of the error magnitudes Mi of e(x) by means of the Forney algorithm [2], which states

Once known the error locations and magnitudes, the error polynomial e(x) can be represented as

and so the transmitted codeword polynomial recovered as c(x) = r(x) + e(x) [NB: addition and subtraction coincide for Galois fields with base 2].
Moreover, the proposed encoder / decoder implementation allows shortened versions of RS codes, i.e. with values of n and k respectively smaller than the conventional 2^m - 1 and 2^m - 1 - 2t. In this case (assuming k and t fixed) the encoder calculates the redundancy after padding 2^m - 1 - 2t - k extra dummy symbols to the actual input message and, then, removes them to retrieve the final shortened codeword. Specularly, the decoder reinserts these extra dummy symbols before starting the decoding procedure.
Besides the encoder / decoder implementation, the MATLAB script also makes available 3 simulations to test the error correction capability of the code, always assuming binary antipodal modulation, AWGN channel and hard-decision detection:
-
1st is a single-run simulation where it is possible to specify as parameters the extended Galois field degree m, the codeword length n, the message length k and the energy-per-bit to noise-spectral-density ratio Eb/N0 over channel and to verify how many bit and symbol errors are introduced by the channel and whether the decoder is able to recover them. An example is displayed in Fig.3, where a typical RS(255,223) for m = 8 is tested. The expected symbol-error correcting capability of this code is t = 16 and, in fact, it proves to able to correct a 15-symbol-corrupted codeword. Moreover, this simulation run shows why RS codes are particularly useful in case of burst noise. A symbol error does not depend on how many bits are wrong within it and this is why ξ > t corrupted bits are still recoverable if they all occur in no more than t symbols [1].

Fig.3 - Single-run simulation in MATLAB
-
2nd is a bit-error-rate (BER) vs Eb/N0 simulation as a function of the maximum number of recoverable errors t, which can be derive as
The results (with n fixed to its maximum value) are displayed in Fig.4 and Fig.5 for m = 4 and 5 respectively. The higher t (i.e. the lower k) the better the coding performances in terms of BER at the expense of an increasing redundancy (or analogously, of a decreasing code-rate Rc, defined as k/n). Moreover, by comparing the two plots it can be highlighted a very important theoretical aspect of RS codes, i.e. that a higher m for almost corresponding values of Rc (curves with the same colour and marker) produces more sloping trends (i.e. better error performance). However, since it can be demonstrated that decoder complexity exponentially grows with m, a practical design and use of RS codes (e.g. on MCUs) shall limit this value.
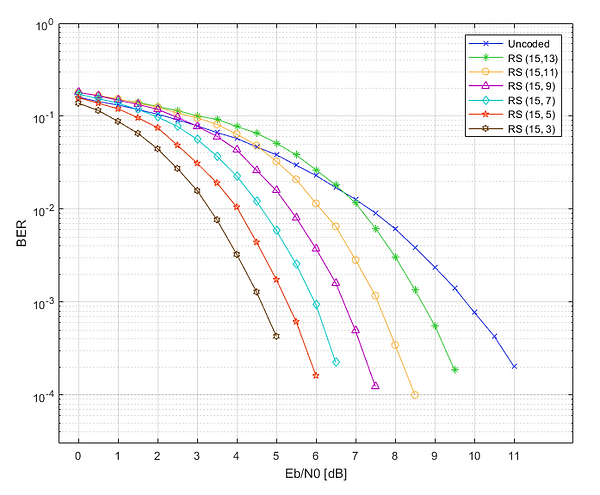
Fig.4 - Coding performance as a function of t for m = 4
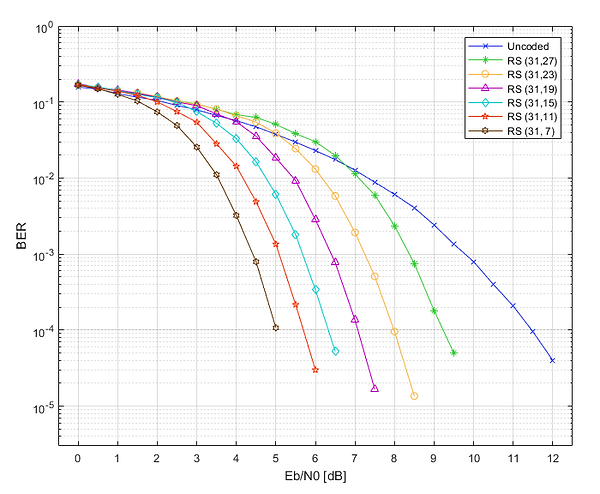
Fig.5 - Coding performance as a function of t for m = 5
-
3rd is a bit-error-rate (BER) vs Eb/N0 simulation among different shortened codes keeping the number of redundancy symbols (i.e. 2t) constant. The results (having fixed m = 6 and t = 8) are displayed in Fig.6. Again, lower values of Rc (corresponding to lower n and k in this case) assure better BER performance.

Fig.6 - Coding performance as a function of the shortened length n for t = 8 and m = 6
After the MATLAB implementation and validation, the encoding and decoding algorithms have been adapted for C/C++ language (only for m = 4 and 8), making it much more efficient and compatible for microcontroller (MCU) operation. In fact, besides other intrinsic advantages, while the MATLAB version works on bits where each of them is by default represented as a double type (i.e. 64 bits), the C/C++ version works on bytes allowing to minimize the memory allocation.
Again, a validation of the code error-correcting capability is provided by simulating a simple binary symmetric channel (BSC) and allowing to set as parameter the probability of error Peb. An example of this simulation is shown in Fig.7, where a source stream (SRC) of 80 bytes for is randomly generated, encoded (ENC) according to the selected m and n parameters, corrupted (ERR) with probability Peb and decoded (DEC). The content of these streams are displayed on the left side of the figure in hexadecimal format. Finally, a check of the number of errors before and after the RS decoder is provided.
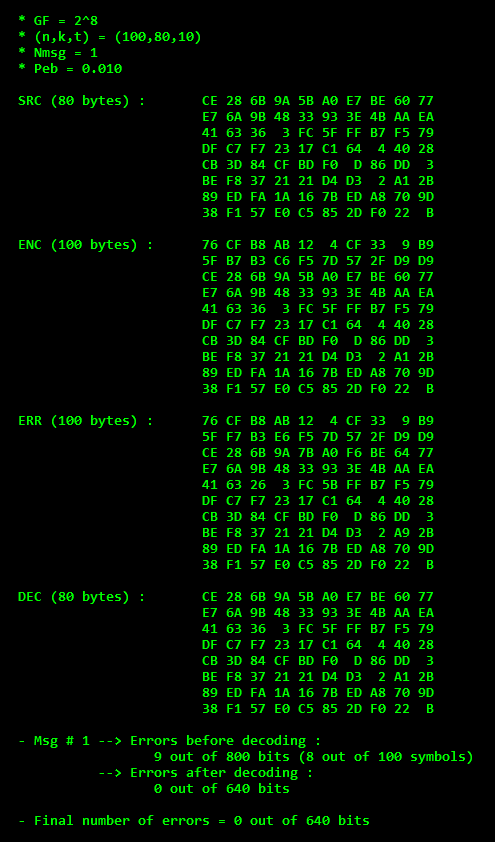
Fig.7 - Single-run simulation in C/C++
Below there are the links through which the aforementioned codes can be free downloaded. For further details and explanations about the practical implementation of the Reed-Solomon encoder / decoder pair take a look at the comments within these files.
WARNING#1: The proposed MATLAB simulations may take several hours to be executed, depending on PC performance.
WARNING#2: The RS.m project has been developed in MATLAB R2017a. Therefore, the correct operation of the script may not be assured with different software versions.
Last update : 06/11/2018
References
[1] B. Sklar and P.K. Ray, Digital Communications, Chapter 8, Pearson Education, 2012
[2] A.Brown, Implementing Reed-Solomon, Duke University, 2011
[3] J.Sankaran, Reed-Solomon Decoder: TMS320C64x Implementation, Texas Instrument, 2000
[4] Wikipedia - Reed–Solomon error correction (link/a)